The Central Tendencies

By Joanne H. -

 The Central Tendencies

Central tendencies = mean, median, and mode.
Published on January 19, 2021

Last modified on 1:03 PM of January 19, 2021

What is a central tendency? In mathematics, central tendency is commonly used in the domain of statistics. A central tendency is "the extent to which statistical values fall around a middle value"[1] .

Basically, there are 3 measures of central tendency: the mean, median, and mode. But what do these 3 strange words represent?

- Mean: the mean is the most common measure of central tendency, and it is often referred as the "average". To calculate the mean, we add all the terms of a data set together, then divide it by the amount of terms there are! You can remember this word with "average". Here is an example:

    5 random students were asked to reveal their science test marks. The marks were: 100, 97, 95, 92, and 90. To calculate the average, we will first add these values together, so we get 100 + 97 + 95 + 92 + 90 = 474. Now we take the result, and divide it by the amount of values there are, so we get 474/5 = 94.8. Therefore, the mean of this data set is 94.8.

-Median: the median is another measure of central tendency, and it's the midmost number in a data set that is placed in an order from least to greatest. To calculate the median, we arrange the data set from least to greatest. Then, we do the elimination process and find the midmost value. If there is an even amount of terms, when there are two numbers in the middle, we usually find the average/mean of those two numbers, and the result is the median. You can remember this word with "middle". Here is an example:

6 students were surveyed for the amount of pets they owned in the past. The results were: 0, 1, 3, 2, 0, and 12. To calculate the median, we would first arrange the number from least to greatest, so we would end up with 0, 0, 1, 2, 3, and 12. Then, we would do the elimination process, and end up with this: 0, 0, 1, 2, 3, 12. Now that we have 1 and 2 in the middle, we would then calculate the mean, which is (1 + 2)/2, and get 1.5. Therefore, the median of this data set is 1.5

-Mode: the mode is another measure of central tendency, and it is the number that occurs the most in a data set. To find the mode, we count how many times a number occurs in a data set, the number that appears the most is the mode. Sometimes, there are 2 or more modes, because sometimes in a data set, there is not any mode (do not put 0 as the answer if there isn't a mode, because 0 is a number, too). You can remember this word with "most". Here is an example:

Two groups of people were interviewed for their shoe sizes. The first group's results were: 3, 6, 4, 8, 2, and 5. To calculate the mode, we need to find the number that appears the most, but all numbers appear the same amount (once), so there is no mode. The second group's results were: 2, 7, 6, 2, 8, 7, and 9. When we calculate the mode for this group, we find that there are two modes: 2 and 7.

"So, which central tendency measure should I use?" Well, the mean is often used when there isn't a number in the data set that's significantly different. The median, on the other hand, is used when there is a number that's significantly different. And the mode? The mode is used when people need to find a common number to represent a data set!

If you have any questions, feel free to contact us via the contact box in our blog.



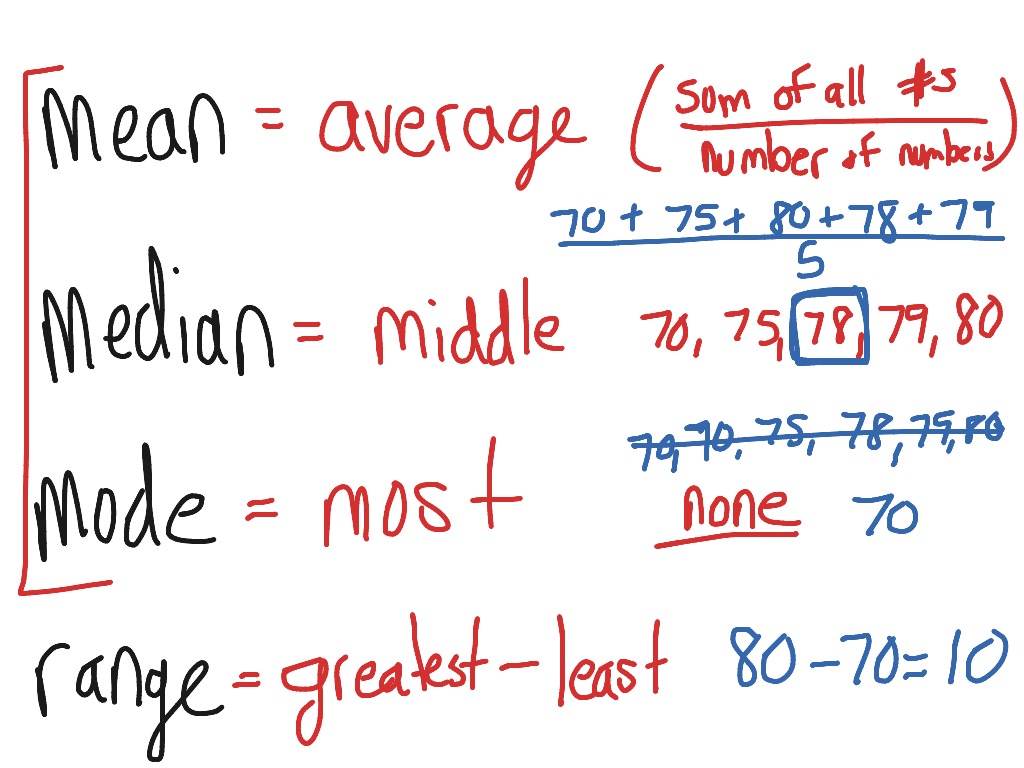
Comments

Post a Comment

Popular posts from this blog

The Functions of Ophiocordyceps unilateralis: a Scientific Article

By Joanne H. -
Image
The Functions of Ophiocordyceps unilateralis: a Scientific Article *do not copy or it will count as plagiarism* Ophiocordyceps unilateralis is just as complicated as it sounds! It's an insect-pathogenic fungal parasite that infects and manipulates ants, and it's also known as zombie ant fungus. Ophiocordyceps unilateralis is found in tropical forests and in many moist places where it can thrive safely. It is one of the many species of Cordyceps, which is a genus full of manipulating fungi, which each infects a different insect. In this case, ants are the victim.  To summarize the process, active Ophiocordyceps unilateralis spores infect ants and force the ants to climb onto the stem of a leaf and bite it with an extreme force so that it wouldn't fall off. Then, the ant dies and a stroma - the main fungus stem - erupts from the back of the ant's head and releases more spores. Although not confirmed, many researchers (like Charissa de Bekker) say that the mind control is ...
click here to see more»

Drug Introduction: Inhalants

By -
Introduction Addiction is considered as a disease, where individuals cannot stop using even when the consequences and conditions are causing serious harms. Addiction is always associated with mental health problems, for instance, depression, because a number of the substances are being used to “self-medicate”. People can develop addictions to alcohol, marijuana, pain killers, cocaine, and tobacco. In this brochure, we will focus on inhalants . Fun fact in a box: Besides addiction, there is another disease which is very similar to it named substance use behaviour. Different from addiction, anyone with substance abuse problems are able to quit or change. So what are inhalants?  Inhalants refers to the numerous substances that people can take only by inhaling, another word for breathing in. When people breathe the substance in, they can get the feeling of “high”. If they do this action repeatedly, there is a chance of getting addicted to the substance. The various types of inhalant...
click here to see more»

The Origin of Life on Earth

By Joanne H. -
Image
                                At one point in life, it is quite plausible that one has pondered about the origin of life. However, it isn’t as likely that they have utilized the inquiry process and chased after their curiosity. How did organisms suddenly emerge on Earth 3.5 billion years ago (Choi, 2017) and how did the basic single-celled organisms evolve into complex life forms about 600 million years ago? This research report contains thorough explanations of selected scientifically-backed theories, as well as visual aids to further elaborate, for those who haven’t researched this. The origin of life on Earth isn’t confirmed, but many theories have been made, and this research will include the more plausible ones: the lightning strike theory, panspermia, the theory of special creation, the theory of primordial soup, and the hydrothermal vent theory. The first theory is the lightning strike theory. This ...
click here to see more»